Roberto D. Pascual-Marqui [CV1, CV2, CV3, CV4, CV5]
-
Networks Tutorial: gets you started with network analysis via functional-ICA
-
New 2018-11-01: Pascual-Marqui, Faber, Kinoshita, Kochi, Milz, Nishida, Yoshimura: A comparison of bivariate frequency domain measures of electrophysiological connectivity. bioRxiv 459503; doi: https://doi.org/10.1101/459503
-
New 2018-02-22: Pascual-Marqui, Faber, Kinoshita, Kochi, Milz, Nishida, Yoshimura: Comparing EEG/MEG neuroimaging methods based on localization error, false positive activity, and false positive connectivity. bioRxiv 269753; doi: https://doi.org/10.1101/269753
-
New 2017-12-18: Pascual-Marqui, Biscay, Bosch-Bayard, Faber, Kinoshita, Kochi, Milz, Nishida, Yoshimura: Measures of time series coupling based on generalized weighted multiple regression. bioRxiv 235721; doi: https://doi.org/10.1101/235721
-
New 2017-08-23: Pascual-Marqui, Biscay, Bosch-Bayard, Faber, Kinoshita, Kochi, Milz, Nishida, Yoshimura: Innovations orthogonalization: a solution to the major pitfalls of EEG/MEG "leakage correction". bioRxiv 178657; doi: https://doi.org/10.1101/178657
-
New 2017-03-23: Pascual-Marqui, Faber, Milz, Kochi, Kinoshita, Nishida, Yoshimura, Kitaura, Ikeda, Ishii: The Cross-Frequency Mediation Mechanism Of Intracortical Information Transactions; bioRxiv 119362; doi: https://doi.org/10.1101/119362
-
New 2016-03-16: Pascual-Marqui, Faber, Kinoshita, Kitaura, Kochi, Milz, Nishida, Yoshimura: The dual frequency RV-coupling coefficient: a novel measure for quantifying cross-frequency information transactions in the brain. arXiv:1603.05343; https://arxiv.org/abs/1603.05343
-
2013-01-21: A measure of association between vectors based on “similarity covariance”
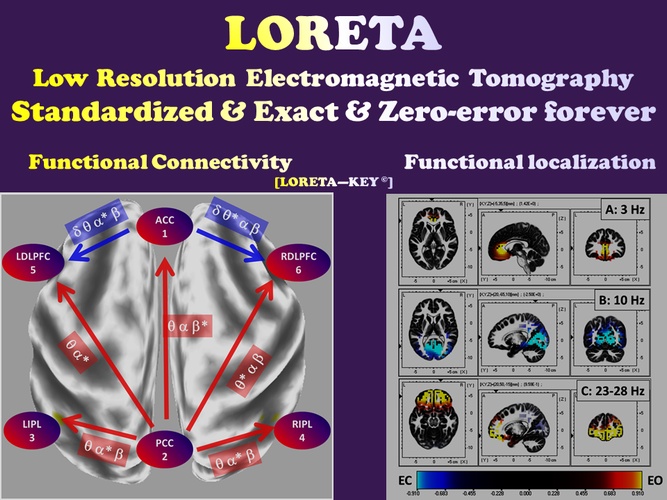
Functional localization and functional connectivity
Non-invasive scalp measurements of electric potential differences (EEG) [as well as magnetic field measurements (MEG)] can be used for estimating the electric neuronal activity distribution (current density vector field) on the cortex. The methods proposed here are LORETA (Pascual-Marqui 1999, Pascual-Marqui et al. 1994), standardized LORETA (sLORETA) (RD Pascual-Marqui 2007, Pascual-Marqui 2002), and exact LORETA (eLORETA) (RD Pascual-Marqui 2007, Pascual-Marqui 2009, R. D. Pascual-Marqui et al. 2011).
Time series of cortical electric neuronal activity estimated with LORETA can be used for estimating cortical connectivity, based on the following informal definition:
“Two places are functionally connected if their activity time series are similar”
See e.g. (Worsley et al. 2005).
However, from a formal point of view, there are many different ways to define similarity between signals.
A collection of new methods proposed here, particularly well-suited for functional (and effective) connectivity measurements using cortical signals estimated with LORETA (or with other tomographies), are:
1. Lagged coherence and lagged phase synchronization (Roberto D Pascual-Marqui 2007, R. D. Pascual-Marqui et al. 2011).
2. Dynamic intracortical connectivity in terms of senders, hubs, and receivers (Pascual-Marqui and Biscay-Lirio 2010).
3. Partial coherence fields (Roberto D Pascual-Marqui et al. 2011).
4. Isolated effective coherence (RD Pascual-Marqui et al. 2014, Roberto D Pascual-Marqui et al. 2014).
Another new method proposed here for discovering generalized functional connectivity, using a different approach, based on methods from the relatively recent branch of statistics known as “functional data analysis” (Ramsay and Silverman 2005), can be found at (Pascual-Marqui and Biscay-Lirio 2011).
All these methods and much more are programmed and available in the alpha LORETA-KEY software package.
LORETA-KEY alpha-software
Download
Read the notes before downloading and extracting and running!
Licence agreement, download, password
Build-date of current alpha software
Click here to see build-date of the current alpha-software
NOTES (open PDF guide)
-
This software is only for advanced users of the sLORETA / eLORETA software package.
-
This is alpha in-house software, not ready for public distribution. It contains many new analysis tools, and it lacks documentation. Use at your own risk, and do not expect immediate help.
-
“LoretaKey.exe” is a “self-extracting” archive.
-
“LoretaKey.exe” is not an installation program. When you run it, the program will allow you to choose a place where it will create a folder named “LoretaKey” with the package. The extraction needs the password shown above.
-
You can only use this software if you have administrator rights.
-
Once extracted, run (as administrator):
“...\LoretaKey\LoretaDesktopShortcutCreator.exe”
which will create a desktop shortcut to the main program, and it will associate files of the type “*.slor” and “*.crss” with the Viewer.
-
Your program version (appearing in the main LORETA program) is given by its build-date, written as an 8 digit number (4 digit year, 2 digit month, 2 digit day) preceded by the letter “v”, as shown in the figure:
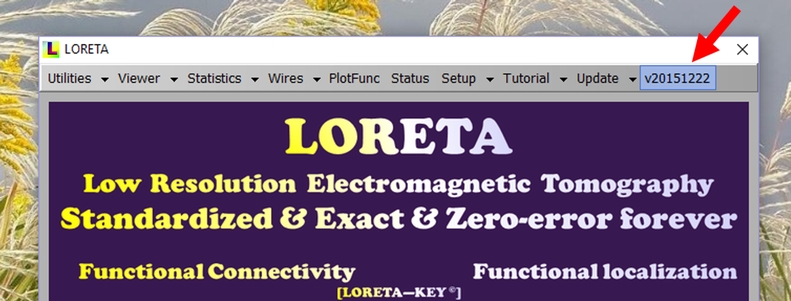
If your program version is older than the current version shown above, you may download the newer version. Ensure you are not running LORETA, then OVERWRITE the previous version with the new package, and repeat step 6 above.
News of 2015-12-22: New tools for assessing cross-frequency coupling within a cortical region, and for cross-frequency information flow between distinct regions
Cross-frequency couplings are assessed by computing complex-valued coherences between Fourier transform coefficients at different frequencies. This methods detects all forms of amplitude-amplitude, phase-amplitude, and phase-phase coupling / information flow. Actually, lagged physiological coupling / information flow is computed (i.e. where low resolution / volume conduction appropriately modeled and eliminated).
A second method uses Hilbert transformation and computes Granger causality measures of connectivity between instantaneous amplitude signals (envelopes) and phase signals, for collection of user-specified frequency bands.
News of 2014-11-10: The resting microstate networks (RMN): cortical distributions, dynamics, and frequency specific information flow
A brain microstate is characterized by a unique, fixed spatial distribution of electrically active neurons with time varying amplitude. It is hypothesized that a microstate implements a functional/physiological state of the brain during which specific neural computations are performed. Based on this hypothesis, brain electrical activity is modeled as a time sequence of non-overlapping microstates with variable, finite durations (Lehmann and Skrandies 1980, 1984; Lehmann et al 1987). In this study, EEG recordings from 109 participants during eyes closed resting condition are modeled with four microstates. In a first part, a new confirmatory statistics method is introduced for the determination of the cortical distributions of electric neuronal activity that generate each microstate. All microstates have common posterior cingulate generators, while three microstates additionally include activity in the left occipital/parietal, right occipital/parietal, and anterior cingulate cortices. This appears to be a fragmented version of the metabolically (PET/fMRI) computed default mode network (DMN), supporting the notion that these four regions activate sequentially at high time resolution, and that slow metabolic imaging corresponds to a low-pass filtered version. In the second part of this study, the microstate amplitude time series are used as the basis for estimating the strength, directionality, and spectral characteristics (i.e., which oscillations are preferentially transmitted) of the connections that are mediated by the microstate transitions. The results show that the posterior cingulate is an important hub, sending alpha and beta oscillatory information to all other microstate generator regions. Interestingly, beyond alpha, beta oscillations are essential in the maintenance of the brain during resting state.
Published as open access pre-print, to be cited as:
"RD Pascual-Marqui, D Lehmann, P Faber, P Milz, K Kochi, M Yoshimura, K Nishida, T Isotani, T Kinoshita. “The resting microstate networks (RMN): cortical distributions, dynamics, and frequency specific information flow”. 2014/November/07. arXiv:1411.1949. http://arxiv.org/abs/1411.1949"
Download at: http://arxiv.org/abs/1411.1949
Links to papers
Generalized Brain Connectivity 2007
eLORETA and Generalized Brain Connectivity 2011
Generalized Cortical Networks 2011
Isolated effective coherence 2014 (iCoh) [technical details ARXIV]
Isolated effective coherence 2014 (iCoh) [Frontiers in Neuroscience]
The resting microstate networks (RMN)
References
Ramsay, J. and Silverman, B. W. (2005) Functional data analysis, 2nd ed., New York:Springer.
News of 2014-06-25: Isolated effective coherence (iCoh): Assessing direct paths of intracortical causal information flow of oscillatory activity
Functional connectivity is of central importance in understanding brain function. For this purpose, multiple time series of electric cortical activity can be used for assessing the properties of a network: the strength, directionality, and spectral characteristics (i.e. which oscillations are preferentially transmitted) of the connections. The partial directed coherence (PDC) of (Baccala and Sameshima 2001) is a widely used method for this problem. The three aims of this study are: (1) To show that the PDC can misrepresent the frequency response under plausible realistic conditions, thus defeating the main purpose for which the measure was developed; (2) To provide a solution to this problem, namely the “isolated effective coherence” (iCoh), which consists of estimating the partial coherence under a multivariate autoregressive model, followed by setting all irrelevant associations to zero, other than the particular directional association of interest; and (3) To show that adequate iCoh estimators can be obtained from non-invasively computed cortical signals based on exact low resolution electromagnetic tomography (eLORETA) applied to scalp EEG recordings. To illustrate the severity of the problem with the PDC, and the solution achieved by the iCoh, three examples are given, based on: (1) Simulated time series with known dynamics; (2) Simulated cortical sources with known dynamics, used for generating EEG recordings, which are then used for estimating (with eLORETA) the source signals for the final connectivity assessment; and (3) EEG recordings in rats. Lastly, real human recordings are analyzed, where the iCoh between six cortical regions of interest are calculated and compared under eyes open and closed conditions, using 61-channel EEG recordings from 109 subjects. During eyes closed, the posterior cingulate sends alpha activity to all other regions. During eyes open, the anterior cingulate sends theta-alpha activity to other frontal regions.
All the technical details can be found in (RD Pascual-Marqui et al. 2014, Roberto D Pascual-Marqui et al. 2014).
For the sake of reproducible research, the software code implementing the methods discussed here (using lazarus free-pascal “http://www.lazarus.freepascal.org”), including the test data as text files, are freely available at [here]. (compressed with 7-zip freeware)
A measure of
association between vectors based on “similarity covariance”
2013-01-21, arXiv:1301.4291 [stat.ME], http://arxiv.org/abs/1301.4291
RD Pascual-Marqui1,2,
D Lehmann2,
K Kochi2,
T Kinoshita3,
N Yamada1
1Department of Psychiatry, Shiga University of Medical Science, Japan; 2The KEY Institute for Brain-Mind Research, University of Zurich, Switzerland; 3Department of Neuropsychiatry, Kansai Medical University, Japan.
The “maximum similarity correlation” definition introduced in this study is motivated by the seminal work of Székely et al on “distance covariance” (Ann. Statist. 2007, 35: 2769-2794; Ann. Appl. Stat. 2009, 3: 1236-1265). Instead of using Euclidean distances “d” as in Székely et al, we use “similarity”, which can be defined as “exp(‑d/s)”, where the scaling parameter s>0 controls how rapidly the similarity falls off with distance. Scale parameters are chosen by maximizing the similarity correlation. The motivation for using “similarity” originates in spectral clustering theory (see e.g. Ng et al 2001, Advances in Neural Information Processing Systems 14: 849-856). We show that a particular form of similarity correlation is asymptotically equivalent to distance correlation for large values of the scale parameter. Furthermore, we extend similarity correlation to coherence between complex valued vectors, including its partitioning into real and imaginary contributions. Several toy examples are used for comparing distance and similarity correlations. For instance, points on a noiseless straight line give distance and similarity correlation values equal to 1; but points on a noiseless circle produces near zero distance correlation (dCorr=0.02) while the similarity correlation is distinctly non zero (sCorr=0.36). In distinction to the distance approach, similarity gives more importance to small distances, which emphasizes the local properties of functional relations. This paper represents a preliminary empirical study, showing that the novel similarity association has some distinct practical advantages over distance based association.
For the sake of reproducible research, the software code implementing all methods discussed here (using lazarus free-pascal “www.lazarus.freepascal.org”), including the test data as text files are freely available, under a Creative Commons Attribution-Noncommercial-ShareAlike license (creativecommons.org/licenses/by-nc-sa/3.0). DOWNLOAD SOFTWARE LINK